|
查看: 1543|回复: 21
|
同 余 问 题
[复制链接]
|
|
|

楼主 |
发表于 18-6-2005 12:11 PM
|
显示全部楼层
找出
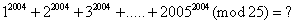 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-6-2005 08:32 PM
|
显示全部楼层
发表于 21-6-2005 08:32 PM
|
显示全部楼层
为什么没人来解啊?
也想请求各位高手做个同余的主题..
因为这里好久没有升精华了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-6-2005 10:21 AM
|
显示全部楼层
发表于 22-6-2005 10:21 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 22-6-2005 02:53 PM
|
显示全部楼层
fritlizt 于 22-6-2005 10:21 AM 说 :
问题是不是说当除于p的时候, 余数会是零???
是 的! 不 过 像 这 类 分 数 “ 模” 的 我 不 大 会 。
[ Last edited by dunwan2tellu on 22-6-2005 at 02:55 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-6-2005 04:04 PM
|
显示全部楼层
发表于 23-6-2005 04:04 PM
|
显示全部楼层
第二题
不好意思,上次打了忘了贴....
多多指教
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 23-6-2005 04:47 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-6-2005 09:18 PM
|
显示全部楼层
发表于 24-6-2005 09:18 PM
|
显示全部楼层
很paiseh..
发现到我的解法有误。
误在 a^4+b^4=(a+b)(a^3 + ... -b^3) 那边...
很对不起
^^" |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-6-2005 09:45 PM
|
显示全部楼层
哈哈。没注意到是 a^4 + b^4 ....看来我两都看漏了  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-6-2005 09:57 PM
|
显示全部楼层
发表于 24-6-2005 09:57 PM
|
显示全部楼层
dunwan2tellu 的"n^4 + (n-1)^4 + (n-2)^4 + (n-3)^4 = 4 ( mod 25 ) " 也有误
就以 n =6 来说 ,和为 2258 = 8 (mod 25)
[ Last edited by 多普勒效应 on 24-6-2005 at 09:59 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-6-2005 10:52 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-6-2005 11:28 PM
|
显示全部楼层
发表于 24-6-2005 11:28 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-6-2005 01:03 AM
|
显示全部楼层
多普勒效应 于 24-6-2005 11:28 PM 说 :
应该是 n=1 (mod5) 吧 ...
有证明吗?
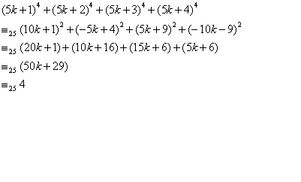 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-6-2005 04:39 PM
|
显示全部楼层
发表于 25-6-2005 04:39 PM
|
显示全部楼层
用回同样的方法
这次检查了好久 ^^"

[ Last edited by 多普勒效应 on 27-6-2005 at 10:09 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-6-2005 11:50 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-7-2005 02:20 AM
|
显示全部楼层
发表于 1-7-2005 02:20 AM
|
显示全部楼层
Hint,
Wilson Theorem
1x2x3x4x...x(p-1)= -1 mod p for p is prime |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 1-7-2005 05:02 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-7-2005 08:50 PM
|
显示全部楼层
1)证明下面的算式可以被10正除

a 为 0 到 9 的 整数 ( [1a] 是个 2 digit number )
2) 找出 7^9999 的末3位数 。
3) 请 问 3333....3333 ( 总 共 3^2005 个 ' 3 ' ) 能 否 被 3^2005 整 除 呢 ?
4) 试 证 明 3^8021 + 6^4011 + 3*16^2005 是 169 的 倍 数 。
5)

[ Last edited by dunwan2tellu on 2-7-2005 at 09:56 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-7-2005 03:41 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-8-2005 08:55 PM
|
显示全部楼层
发表于 3-8-2005 08:55 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 2-7-2005 08:50 PM 发表
1)证明下面的算式可以被10正除

a 为 0 到 9 的 整数 ( [1a] 是个 2 digit number )
2) 找出 7^9999 的末3位数 。
3) 请 问 333 ...
3)^9999(mod 1000)=(7^9)^1111(mod 1000)
=607^1111(mod 1000)
=(607^11)^101(mod 1000)
={(607^3)^3x607^2}^101(mod 1000)
=(543^3x449)^101(mod 1000)
=143^101(mod 1000)
=(143^4)^25(143)(mod 1000)
=(601^25)(143)(mod1000)
=(601^2x601^3)^5(143)(mod1000)
={201x801}^5(143)(mod1000)
=001^5(143)(mod1000)
=143(mod1000)
the last 3 digit is 143
5)10^10(mod7)=4(mod7)*1
4^(mod7)=4(mod7)*2
10^10=10^100
=(10^10)^10
=4^10(mod7)
=4(mod7)
10^100mod7=[(10^10)^10]^10mod7
=(4^10)^10mod7
=4^10mod7
=4mod 7
from *1&*2deduced:
(10^10+10^100+10^1000+.......+10^10^2005)(mod7)
=[4+4^10+(4^10)^10+.......+4^10^2004](mod7)
=(4+4+4+4+4......+4)(mod7)
(there is a total of 2005 of 4's)
=(4x2005)(mod7)
=(4x3)(mod7)
=12(mod7)
=5(mod7)
k=5 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|