|
|
 发表于 24-9-2004 02:08 PM
|
显示全部楼层
发表于 24-9-2004 02:08 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 02:47 PM
|
显示全部楼层
发表于 24-9-2004 02:47 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-9-2004 04:48 PM
|
显示全部楼层
发表于 24-9-2004 04:48 PM
|
显示全部楼层
fritlizt 于 03-09-2004 14:47 说 :
这是几时的题目???
这是今天的题目:
24/09/2004,星期五
高中(B17) 设 {a} 为任意的等差数列,其公差为 d,而且{a}的每一项皆是整数。
若 w,x,y,z 为{a} 连续的四项。
证明:wxyz + d^4 是个完全平方数。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-9-2004 10:21 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-9-2004 02:54 PM
|
显示全部楼层
发表于 27-9-2004 02:54 PM
|
显示全部楼层
27/09/2004,星期一
初中(A19) 不可用计算机,找出下列的值:
√{5 + √(21)} + √{5 - √(21)}
(答案以根号(surd form)来表示)
{√[5 + √(21)] + √[5 - √(21)]}^2
=[5 + √(21)]+2√[5 + √(21)]√[5 - √(21)]+[5 - √(21)]
=10+2√[25-21]
=14
所以,√{5 + √(21)} + √{5 - √(21)}=√14 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-9-2004 03:02 PM
|
显示全部楼层
发表于 27-9-2004 03:02 PM
|
显示全部楼层
我们应该只拿+ve value吧...
因为根号之和是+ve value的
不知道这讲法是否完全正确? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 27-9-2004 03:25 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-9-2004 05:09 PM
|
显示全部楼层
发表于 28-9-2004 05:09 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-9-2004 06:20 PM
|
显示全部楼层
发表于 28-9-2004 06:20 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-9-2004 06:21 PM
|
显示全部楼层
发表于 28-9-2004 06:21 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-9-2004 06:58 PM
|
显示全部楼层
发表于 28-9-2004 06:58 PM
|
显示全部楼层
28/09/2004,星期二
初中(A20) 如图,角 ABC 及 角 BDA 皆是直角。
若 v + w = 35,x + y = 37,
求 y 之值。
(待解)
(答案:)
(解对者:)
已知,v + w = 35,x + y = 37
角 ABC ,x^2=w^2+v^2
角 ABC 及 角 BDA 的面积相同,xy/2=wv/2
x^2=w^2+v^2
x^2=(w+v)^2-2wv
x^2+2wv=35^2
x^2+2xy=35^2(xy=wv)
(x+y)^2-y^2=35^2
所以,y^2=37^2-35^2
y^2=144
y=12(-ve value 不合题意) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 29-9-2004 09:36 AM
|
显示全部楼层
eeCyang 于 28-9-2004 06:20 PM 说 :
真的是这样吗?
那为什么6不行呢?
不好意思,请多指教.
sinchee 讲的没错!!
试试用一点点的代数知识便可!!
我本身的做法是:
从可能的号码{0,2,4,6,8}
去掉{2,8}(因为没有完全平方数的个位数是如此的!!)
再去掉{0}(若是"0",那么十位数也肯定是"0"!)
最后去掉{6}(因为 66 不能被 4 整除。。。(想想。。。)) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 09:38 AM
|
显示全部楼层
发表于 29-9-2004 09:38 AM
|
显示全部楼层
不好意思,有点小错误..(角 ABC 及 角 BDA 的面积相同)
应该是角 ABC 的面积的找法有2种 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 29-9-2004 09:41 AM
|
显示全部楼层
两天过去了。。。有两题被解决了!!
各位,"革命"尚未完成!!请再努力!!
19/09/2004,星期日
大专(C5) 某个醉汉目前在位置 "5",他的家在位置 "8",而位置 "0" 则是断崖。
由于他分不清方向,设他每次移动一单位,且只走向左或向右,而每次向左或向右的机率皆为 1/2。
若到位置 "8",则家人迎接他(安全抵达)。
若到位置 "0", 则跌入断崖。。。(无法继续行程)
求此醉汉安全回到家的机率。
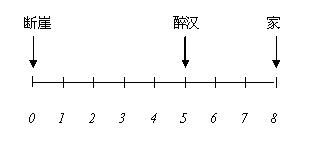 (待解) (待解)
26/09/2004,星期日
大专(C6) 如下图,在单位圆(即半径为 1)的圆周上取 5 个点。
(将这5点连起来,可形成正五边形)
现在,5 点中任选 1 点,将此点接连其余 4 点,得四个线段.
设这四个线段的长度分别为 a,b,c,d。
求证: abcd = 5
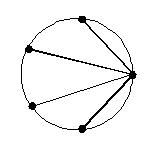 (待解) (待解)
请大家再试试吧!
flash 网友,飞鱼兄,鸟哥,若有空的话,请来玩玩!!
[ Last edited by pipi on 29-9-2004 at 09:45 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 09:43 AM
|
显示全部楼层
发表于 29-9-2004 09:43 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 01:17 PM
|
显示全部楼层
发表于 29-9-2004 01:17 PM
|
显示全部楼层
若 x < -2,试简化 |1-|1+x||。
我试试看。。
若 1+x = a
那么, a < -1
1+x < -1
|1+x| > 1
若 |1+x| = b > 1
1-b < 0
|1-b| > 0
那么 | 1 - |1+x| | > 0
对吗? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 29-9-2004 01:27 PM
|
显示全部楼层
史奴比{^_^} 于 29-9-2004 01:17 PM 说 :
若 x < -2,试简化 |1-|1+x||。
我试试础!?
若 1+x = a
那么, a < -1
1+x < -1
|1+x| > 1
若 |1+x| = b > 1
1-b < 0
|1-b| > 0
那么 | 1 - |1+x| | > 0
对吗?
这不叫"简化"吧!!
不管 x 是什么,
| 1 - |1+x| | > 0 都是对的!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 02:21 PM
|
显示全部楼层
发表于 29-9-2004 02:21 PM
|
显示全部楼层
啊。。 对hor..
不好意思。 ^_^
真的好笨 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 03:03 PM
|
显示全部楼层
发表于 29-9-2004 03:03 PM
|
显示全部楼层
pipi 于 29-9-2004 13:27 说 :
这不叫"简化"吧!!
不管 x 是什么,
| 1 - |1+x| | > 0 都是对的!!
okey..
答案是 |2+x| |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-9-2004 03:46 PM
|
显示全部楼层
发表于 29-9-2004 03:46 PM
|
显示全部楼层
史奴比{^_^} 于 29-9-2004 03:03 PM 说 :
okey..
答案是 |2+x|
虽然我也是这样想...
但应该没那么简单吧.. |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|