中学数学讨论区-限于课业的问题

fritlizt

好像很静。 丢颗炸弹进来热闹热闹一下。




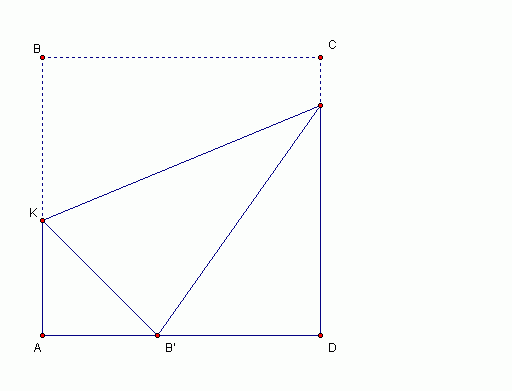
ABCD 是一个正方形的纸。
AB = BC = CD = DA = 10cm
若我把 B 点折下来放在边 AD 上。
找出 AB' 的长度以让面积KAB'是最大。

山羊座

1. 设 cos x + sin x =2,   (0<x< 90)  
   求 cos x + sin x = ?

山羊座

山羊座 于 26-8-2004 01:52  说 :
1. 设 cos x + sin x =2,   (0<x< 90)  
   求 cos x + sin x = ?

对不起
打错题目
应为
   设 cos x + 3sin x =2,   (0<x< 90)  
   求 cos x + sin x = ?

山羊座

希望解题者可以把过程写出来，
最好在不需应用calculator 的情况下

pipi

山羊座 于 26-8-2004 01:53 AM  说 :
   设 cos x + 3sin x =2,   (0<x< 90)  
   求 cos x + sin x = ?

我们可设
cos x + sin x = c > 0 (因为 0<x<90 度)
那么 (cos x + sin x)^2 = c^2
所以 (cos x)^2 + (sin x)^2 + 2sin x = c^2
       1 + 2 sin x = c^ 2
      2 sin x = c^2  -  1
由题目：
cos x + 3sin x =2,
(cos x + sin x) + (2 sin x) = 2
       c + c^2 - 1 = 2
       (c + 1/2)^2 =  3 + 1/4 = 13/4
       c = -1/2 + sqrt(13)/2 or       -1/2 - sqrt(13)/2（不可能）
所以   c = {sqrt(13)-1}/2
证毕！！

山羊座

pipi 于 26-8-2004 14:20  说 :

我们可设
cos x + sin x = c > 0 (因为 0<x<90 度)
那么 (cos x + sin x)^2 = c^2
所以 (cos x)^2 + (sin x)^2 + 2sin x = c^2
       1 + 2 sin x = c^ 2
      2 sin x = c^2  -  1
由题目：
...

Is (cos x + sin x)^2 = (cosx)^2 + (sinx)^2 + 2sinxcosx
                     = 1 + sin2x ??

So I thought your solution was wrong
And the answer is  [4+ (6)^1/2]/5

pipi

山羊座 于 26-8-2004 03:36 PM  说 :
Is (cos x + sin x)^2 = (cosx)^2 + (sinx)^2 + 2sinxcosx
                     = 1 + sin2x ??
So I thought your solution was wrong
And the answer is   ...

哈，答得太快，一时弄错了。。。paise, paise!!
再来一次：
设 a = sin x > 0, b = cos x >0， (因为0<x<90 度)
我们有 a^2 + b^2 = 1
由 a + 3 b = 2
3b  = 2 - a
9b^2 = 4 - 4a + a^2
9 (1 - a^2) = 4 - 4a + a^2
10a^2 - 4a - 5 = 0
所以 a = {2 ± 3sqrt(6)}/10
因为 a>0
选 a = {2 + 3sqrt(6)}/10
a^2 = {4 + 9(6) + 12sqrt(6)}/100
1 - b^2 = {58 + 12sqrt(6)}/100
b^2 = {42 - 12sqrt(6)}/100
     = {(6 - sqrt(6))/10)}^2
  b  = ±(6 - sqrt(6))/10)
因为 b>0
选 b = {6 - sqrt(6)}/10
所以 a + b = {2 + 3sqrt(6)}/10 + {6 - sqrt(6)}/10
           = {8 + 2sqrt(6)}/10
           = {4 + sqrt(6)}/5
完毕！！

啊蛋

Given  11x^2- 8xy + 5y^2= 32 ,
        x^2+ y^2        = 8 ,
deduce that 7x^2- 8xy + y^2= 0, and
hence , find all the pairs of values of x, y that satisfy the given equation.

请问这题有谁会？我只会 first part , second part 不会  

[ Last edited by 啊蛋 on 26-8-2004 at 11:19 PM ]

pipi

啊蛋 于 26-8-2004 11:14 PM  说 :
Given  11x^2- 8xy + 5y^2= 32 ,
        x^2+ y^2        = 8 ,
deduce that 7x^2- 8xy + y^2= 0, and
hence , find all the pairs of values of x, y that satisfy the given equation.

请问这题有谁会？我只会  ...

第二部分：
7x^2- 8xy + y^2= 0
(7x-y)(x-y)=0
y = x    or    y = 7x

当 y = x， 由
x^2+ y^2  = 8
x^2+ x^2  = 8
2x^2 = 8
x^2 = 4
x = ±2

当 y = 7x， 由
x^2+ y^2  = 8
x^2+ (7x)^2  = 8
50x^2 = 8
x^2 = 4/25
x = ±2/5

所以，其解为(x,y) = (2,2),(-2,-2),(2/5,14/5),(-2/5,-14/5)

啊蛋

thank you a lot .. hooh

山羊座

QUESTION :
长方体的一条对角线与各个面所成的角分别为 a,b,c ，
则 (cosa)^2 + (cosb)^2 + (cosc)^2 = _________ .    (ANSWER : 2)
Please show the solution for this question!

pipi

山羊座 于 28-8-2004 03:09 PM  说 :
QUESTION :
长方体的一条对角线与各个面所成的角分别为 a,b,c ，
则 (cosa)^2 + (cosb)^2 + (cosc)^2 = _________ .    (ANSWER : 2)
Please show the solution for this question!

我想你的问题应该是＂看不到＂它要的角度吧！！
试试从以下的图得到一些资料，其他的你自己来吧。。。
应该不难的！！


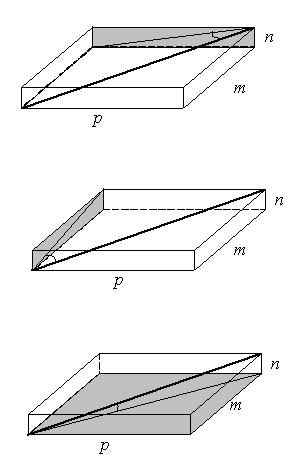
[ Last edited by pipi on 29-8-2004 at 09:39 PM ]

sooshi

persamaan kuadratik ax^2+(a+b)x+b=0 mempunyai dua punca nyata yang berbeza.
(a)Diberi salah satu puncanya ialah 4.Cari punca yang satu lagi.
(b)jika b^2-a^2=3(a-b)dan a 不等于 b ,cari nilai bagi a dan b

Answer:
(a) -1
(b)a= 1, b=-4

谁可以教我做这题（最好有算法和解释）

chwk87

a) katakan punca yg satu lagi= k
maka,4+k=-(a+b)/a  dan  4k=b/a
     4+k= -1-a/b
        =-1-4k
       5k=-5
        k=-1

b)b^2-a^2=3(a-b)
  (b+a)(b-a)=-3(b-a)
        b+a=-3 ------------(A)
     4k=b/a
     4(-1)=b/a
        b=-4a --------------(B)
gantikan (B) dlm (A)
-4a+a=-3
   -3a=-3
     a=1
gantikan a=1 dlm (B)
   b=-4(1)
    =-4

sooshi

chwk87 于 31-8-2004 01:44  说 :
a) katakan punca yg satu lagi= k
maka,4+k=-(a+b)/a  dan  4k=b/a
     4+k= -1-a/b
        =-1-4k
       5k=-5
        k=-1

b)b^2-a^2=3(a-b)
  (b+a)(b-a)=-3(b-a)
        b+a=-3 ----------- ...

谢谢!!!!!

sooshi

请问这几题如何解答？

1. Diberi persamaan kuadratik (m-3)x^2-(m^2-m-12)x+(3m-1)(m+3)=0. Cari nilai-nilai m jika
(a)salah satu punca bernilai negatif punca yang satu lagi.
(b)salah satu punca merupakan salingan punca yang satu lagi.

2. Cari nilai yang mungkin bagi K jika garis lurus y=7+k ialah tangen kepada lengkungan y=2x^2-3x+2.Seterusnya cari titik di mana sentuhan berlaku.

3. Diberi persamaan kuadratik rx^2-(3p+1)x-(p+5)=0 dan r不等于0.Nyatakan syarat yang harus dipatuhi oleh p supaya persamaan kuadratik ini mempunyai dua punca nyata yang sama.

4. Diberi bahawa A dan B ialah punca-punca bagi persamaan 2x^2=3x-1 dan A>B.
(a)Bentukkan persamaan kuadratik yang mempunyai punca-punca A^4+4B^2+1 dan 16B^2-3A^2.
anwers:

1.(a) m=-3atau4
  (b) m=0atau -2(1/3)
2.k=-6(1/8);(3/4,7/8)
3.p不等于-1/3
4.x^2-4x+3=0

对不起，太多题不会做
请各位高手指点！！！！！！
谢谢！！！

wanmeijuxie

不好意思，可以请问这题应该怎么解吗？
when the polynomial p(x)is devided by (x-3) the remainder is 3,
          and when p(x) is devided by (x+2) the remainder is 13.
Find the remainder when the polynomial is devided by (x-3)(x+2)

chwk87

1 a) katakan satu punca=a,maka punca yg satu lagi=-a
     h.t.p = a+(-a) = (m^2-m-12)/(m-3)
             0=m^2-m-12
          (m-4)(m+3)=0
      maka,m=4 @-3

   b) katakan satu punca=a ,maka punca yg satu lagi=1/a
     h.D.p.=a(1/a) =(3m-1)(m+3)/(m-3)
            m-3=3m^2+8m-3
           3m^2+7m=0
          m(3m+7)=0
        maka,m=0 @ -7/3

2)y=7+k -----------1
y=2x^2-3x+2 ----------2
gantikan 1 dlm 2
maka 2x^2-3x-5-k=0
     b^2-4ac=0
   kamu akn dpt
       k=-49/8
kemudian gantikan nilai k dlm (1) dan selesaikan pers serentak itu, kamu akn dpt jwpnya.

3)my own answer is p should be equel to -29/3
may be i did wrong.

4)2x^2-3x+1=0
  A+B=3/2
    A=3/2-B -----1
  AB=-1/2-------2
selesaikan,maka kamu akn dapat B=1/2 @ 1
o krn A>B, maka B=1/2 dan A=1

H.T.P= A^4+4B^2+1+16B^2-3A^2.
     =A^4+20B^2+1-3A^2
      =1^4+ 20(1/2)^2+1-3(1)^2
      =4

H.D.P=(A^4+4B^2+1)(16B^2-3A^2)
     =(1^4+4(1/2)^2+1)(16(1/2)^2-3(1)^2)
     =3.

maka x^2-(H.T.P)x+(H.D.P)=0
     x^2-4x+3=0

Form 6: vector
A lane crosses with another lane at 0 at an angle of 60. A boy, A, is 300m from O in one of the lanes and another boy, B, is 400m from O in another lane. Both the boys run towards O simultaneously, with A moving at a speed of 15km/h and B at a speed of 12km/h. Find the closest distance between A and B.
answer is 151m

pipi

晴天蓝 于 1-9-2004 09:38 PM  说 :
Form 6: vector
A lane crosses with another lane at 0 at an angle of 60. A boy, A, is 300m from O in one of the lanes and another boy, B, is 400m from O in another lane. Both the boys run towards O ...

我的答案：