数学训练～每日一题

快乐

24/08/2004，星期二
初中(A5) 某年的六月份里有三个星期三是奇数，该月的13日是星期几？ （待解）

我也知道是星期一。
因为下个月(九月份)的月历就符合了这个问题。

可是，如果用算的，
是怎样演变出来的？？？
可不可以解说一下？

[ Last edited by 快乐 on 25-8-2004 at 05:54 PM ]

fritlizt

不可用计算机（或对数表(sifir)），决定以下的最大值（并说出原因）：
(a) 6^100　  (b) 5^200　(c) 4^300  (d) 3^400   (e) 2^500  

6^100 < 9^100 = 3^200
6^100<3^400

1.4^300 = 2^600 = 8^200
2.3^400 = 9^200
3.5^200 = 5^200
4.2^500 = [2^(5/2)]^200

比较  8,9,5,及 2^(5/2)
9 比较大。

所以  3^400  比较大。

chwk87

某年的六月份里有三个星期三是奇数，该月的13日是星期几？

6月 有 30天 ， 所 以 有 4个 星 期 ， 也 就 是 有 4个 星 期 三。 不 过 只 有  两 个 星 期 三 是 奇 数。  所 以 要 有 多 一 个 星 期 三。 而 这 个 星 期 三 将 会 落 在  剩 下 的 两 天 。因 此 ，6月 1日 或 2日 必 须 是 星 期 三，  以 便 有 5个 星 期 三 。由 于 星 期 三 是 奇 数，  所 以 6月 1日 必 须 是 星 期 三。 因 此 8日 ， 15日 也 是
星 期 三。 15日 再 减 两 日 就 是 星 期 一 。

希 望 可 以 解 答 你 的 疑 问 。

辉文

pipi 于 24-8-2004 08:33  说 :
上个礼拜未解的题目：

我在这里给个提示：
(i)   若 x,y,z > 0, 则 x/y > x/(y+z)
(ii)　试试考虑 ∫p(x) dx （由 x=-1 至 x=1）　

大家加油！！

[ Last edited by pipi on 24-8-2004 at 08:34 ...

pipi，关于星期日p(x)=0那题的解，我的朋友也有解：

原题目：

大专(C1) 设 p(x) = a + bx + 3cx^2 + dx^3 + 5ex^4 为一实数多项式。
         已知 a + c + e = 0，求证 p(x) = 0 在区间 [-1,1] 中有一实根。

p(x) = a + bx + 3cx^2 + dx^3 + 5ex^4
积分 p(x)，得到f(x)

f(x)=ax + bxx/2 + cx^3 + dx^4/4 + ex^5
已知a+c+e=0

f(1)=a + b/2 + c + d/4 + e=b/2+d/4
f(-1)=-a + b/2 - c + d/4 - e=b/2+d/4
==> f(1)=f(-1)
==> f'(x)=(f(1)-f(-1))/2=0 在区间 [-1,1] 中有一實根。 (叫"均值定理"的樣子)
==> p(x)=0 在区间 [-1,1] 中有一實根。

虽然有点类似jwyong说的两片面积相等。但是我不晓得她的方法是否正确，如果正确的话，也不算是我做的。还有可以完整的解释什么是均值定理，英语叫做什么？（不好意思，我的朋友是台湾人，所以她用的中文名词我有点不明白）

微中子

应该是Mean value theorem吧?

我是从她的做法猜的.

快乐

chwk87 于 25-8-2004 08:41 PM  说 :
因 此 ，6月 1日 或 2日 必 须 是 星 期 三，  以 便 有 5个 星 期 三 。由 于 星 期 三 是 奇 数，  所 以 6月 1日 必 须 是 星 期 三。 因 此 8日 ， 15日 也 是
星 期 三。 15日 再 减 两 日 就 是 星 期 一 。

如果6月2日是星期三，
那么就会变成三偶两奇，不符合题目的要求了。
所以6月1日一定(也必须)是星期三。

你的解答太完美了。
我完全收到，谢谢分享。

pipi

辉文 于 26-8-2004 01:16 AM  说 :
p(x) = a + bx + 3cx^2 + dx^3 + 5ex^4
积分 p(x)，得到f(x)
f(x)=ax + bxx/2 + cx^3 + dx^4/4 + ex^5
已知a+c+e=0

f(1)=a + b/2 + c + d/4 + e=b/2+d/4
f(-1)=-a + b/2 - c + d/4 - e=b/2+d/4
==> f(1)=f(-1)
==> f'(x)=(f(1)-f(-1))/2=0 在区间 [-1,1] 中有一實根。 (叫"均值定理"的樣子)
==> p(x)=0 在区间 [-1,1] 中有一實根。

这个方法完全正确！！
均值定理 就是 Mean Value Theorem （就如微兄所讲的）。

fritlizt 于 24-8-2004 02:29 PM  说 :
∫p(x) dx = 0；
在 -1 与 1 之间， 有一部分的面积是positive 的。 有一些是negative 的。
我不懂有多少。 不过至少会有一个positive 及一个 negative .
所以：　-1 与　1 之间至少有一个实数根。

它也可以全部为 ＂零＂！(p/s:面积不能是 negative!!!)
想法是对的，不过这样的讲法不太严谨吧。。。
或者我们可用反证法：
若 p(x) = 0 for all x in [-1,1]，那么原题得证！
假设 p(x)≠0 for all x in [-1,1]。

那么(i)  p(x) > 0 for all x in [-1,1] 或者
    (ii) p(x) < 0 for all x in [-1,1]。
我们将分别从 (i)与(ii) 得到 ∫p(x) dx > 0 及 ∫p(x) dx < 0
（这与我们的计算 ∫p(x) dx = 0 产生矛盾！！）
所以存在着 r, s in [-1,1] 令到 p(r）p(s) <0 ，
由于 p(x) 是连续方程，
就存在着 k in [-1,1] 令到 p(k)=0 。(Intermediate Value Theorem)
证毕！

[ Last edited by pipi on 27-8-2004 at 07:44 AM ]

20/08/2004，星期五
高中(B2) a,b,c,d 为任意正数，设 S = a/(a+b+d) + b/(a+b+c) + c/(b+c+d) + d/(a+c+d)
         求证：  1 < S < 2

因为a,b,c,d 为任意正数，
a/(a+b+d) > a/(a+b+c+d)
b/(a+b+c) > b/(a+b+c+d)
c/(b+c+d) > c/(a+b+c+d)
d/(a+c+d) > d/(a+b+c+d)
所以
S > a/(a+b+c+d) + b/(a+b+c+d) + c/(a+b+c+d) + d/(a+b+c+d) = 1


而且，
a/(a+b+d) < a/(a+b)
b/(a+b+c) < b/(a+b)
c/(b+c+d) < c/(c+d)
d/(a+c+d) < d/(c+d)
所以
S < a/(a+b) + b/(a+b) + c/(c+d) + d/(c+d) = 2

故  1 < S < 2

不好意思，其实我超龄了。。。

[ Last edited by sinchee on 26-8-2004 at 03:04 PM ]

pipi

对了啦！！
sinchee，最近失踪了？？？
电脑坏了？？？

fritlizt

pipi 于 26-8-2004 01:59 PM  说 :

它也可以全部为 ＂零＂！(p/s:面积不能是 negetive!!!)
想法是对的，不过这样的讲法不太严谨吧。。。
或者我们可用[color= ...

对不起。忘了说 negetive 的面积是代表在x-axis 下的面积。

pipi

快乐 于 25-8-2004 05:29 PM  说 :
x=y(a-b)/(b-c)
z=y(c-a)/(b-c)
x+y+z = y(a-b)/(b-c) + y + y(c-a)/(b-c)
这题的答案应该是。。。
x+y+z= 0

备注：没发现到。。。已经有人抢先回答了。

别人答了也无所谓，大家分享分享！！欢迎光临！！

fritlizt 于 25-8-2004 06:31 PM  说 :
6^100 < 9^100 = 3^200
6^100<3^400

1.4^300 = 2^600 = 8^200
2.3^400 = 9^200
3.5^200 = 5^200
4.2^500 = [2^(5/2)]^200

比较  8,9,5,及 2^(5/2)
9 比较大。
所以  3^400  比较大。

答案完全正确！！
我们也可以一开始便考虑：
6 < 5^2 < 2^5 < 4^3 < 3^4
(6)^100 < (5^2)^100 < (2^5)^100 < (4^3)^100 < (3^4)^100
所以 6^100 < 5^200 < 2^500 < 4^300 < 3^400

chwk87 于 25-8-2004 08:41 PM  说 :
6月 有 30天 ， 所 以 有 4个 星 期 ， 也 就 是 有 4个 星 期 三。 不 过 只 有  两 个 星 期 三 是 奇 数。  所 以 要 有 多 一 个 星 期 三。 而 ...

你的解释完全正确！！赞！！再接再厉！！

chwk87

是 不 是 540 度﹖

loveissecret

直觉肉眼看上去有没有可能是360度?
因为回到原位就是绕一圈-360度..

实际上,我还要试一下其他方法.

pipi

chwk87 于 27-8-2004 10:28 AM  说 :
是 不 是 540 度﹖

loveissecret 于 27-8-2004 02:27 PM  说 :
直觉肉眼看上去有没有可能是360度?
因为回到原位就是绕一圈-360度..

实际上,我还要试一下其他方法.

这两个答案看似有它的道理，但却不正确！！
请再试试！！

微中子

看来好像是1080

高中(B1) 已知 (y+z)/(b+c) = (z+x)/(c+a) = (x+y)/(a+b)，
         求证  (x+2y-3z)/(4x+5y-6z) = (a+2b-3c)/(4a+5b-6c)

虽然已经解了，但还是想玩玩。。。

设(y+z)/(b+c) = (z+x)/(c+a) = (x+y)/(a+b) = k
则(y+z) = k(b+c)   (i)
  (z+x) = k(c+a)   (ii)
  (x+y) = k(a+b)   (iii)

(i)+(ii)+(iii),  x+y+z = k(a+b+c)   (iv)
(iv) - (i),      x = ka
(iv) - (ii),     y = kb
(iv) - (iii),    z = kc

因此(x+2y-3z)/(4x+5y-6z)=(ka+2kb-3kc)/(4ka+5kb-6kc)
                        =(a+2b-3c)/(4a+5b-6c)

[ Last edited by sinchee on 28-8-2004 at 11:50 AM ]

pipi 26/08/2004，星期四
高中(B4) 求证
         (i)        数列 11,111,1111,...
         (ii)       数列 44,444,4444,...
            中的每一项都不是完全平方数。

(i)      
设 x^2 = 1111...
则 x必为一奇数，
若 x = 2k + 1
  x^2 = 4k^2 + 4k + 1 = 1111...
  4(k^2 + k) = 111...110

但，
111...110 不能被4整除
所以1111... 不是完全平方数


(ii)      
设 x^2 = 4444...
则 x必为一偶数，
若 x = 2k
  x^2 = 4k^2 = 4444...
  k^2 = 1111...
因为1111... 不是完全平方数
所以4444... 也不是完全平方数

[ Last edited by sinchee on 28-8-2004 at 12:41 PM ]

pipi 27/08/2004，星期五
高中(B5) 如图，四个一角钱硬币，其中蓝色的沿着其他三个滚了一圈，直到回到原位为止。
         请问蓝色的硬币，共转了多少度？

我的答案也是1080度。
拿三个一角来转一下就懂了。。。

pipi 28/08/2004，星期六
高中(B6) 设 n (>3) 为自然数且 n, n+2 为质数。
         求证 n+1 是 6 的倍数。

因为 n, n+2 为质数，
所以 n+1为偶数。
也因为 n, n+2 为质数，不能被3整除，
所以 n+1 能被3整除。

故 n+1 是 6 的倍数。

pipi

微中子 于 28-8-2004 06:25 AM  说 :
看来好像是1080

sinchee 于 28-8-2004 12:35 PM  说 :
我的答案也是1080度。
拿三个一角来转一下就懂了。。。

没错！答案正是 1080度。
二位真聪明！！
那么如果是以下的情况呢？？

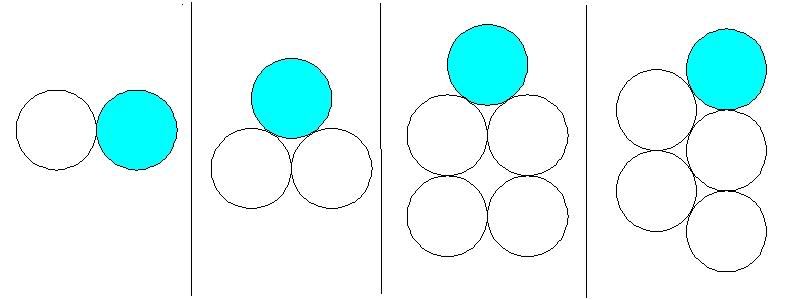
有没有一般性的解法？？