|
|
 发表于 12-7-2005 06:00 PM
|
显示全部楼层
发表于 12-7-2005 06:00 PM
|
显示全部楼层
|
高中生在独中来说是form 4 到form 6 , 国中则是form 3 到form 5 . |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-7-2005 11:57 PM
|
显示全部楼层
发表于 14-7-2005 11:57 PM
|
显示全部楼层
用定积分求
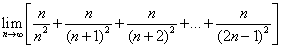
之值 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-7-2005 02:35 PM
|
显示全部楼层
发表于 15-7-2005 02:35 PM
|
显示全部楼层
多谱勒的问题是用quadrature来做吗?酱的话应该是 1/2

[ 本帖最后由 dunwan2tellu 于 15-7-2005 02:59 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-7-2005 12:09 PM
|
显示全部楼层
发表于 16-7-2005 12:09 PM
|
显示全部楼层
这里也有一些quadrature的题目 ....
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-7-2005 11:27 PM
|
显示全部楼层
发表于 17-7-2005 11:27 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 15-7-2005 02:35 PM 发表
多谱勒的问题是用quadrature来做吗?酱的话应该是 1/2

看不明白喔...
為什麼會醬的 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-7-2005 12:44 AM
|
显示全部楼层
发表于 18-7-2005 12:44 AM
|
显示全部楼层
它的concept是要integrate一个函数f(x),范围在a到b (i.e. 0到1),就把 a ->b 的interval 分成 n 个区,使每个区的宽=(b-a)/n 。那么f(x)的积分也相等于把f(x)分为n个长方形的面积的和 。其和为 lim{ Sum f(x_k)h } where h = (b-a)/n
[ 本帖最后由 dunwan2tellu 于 18-7-2005 12:46 AM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-7-2005 04:21 PM
|
显示全部楼层
发表于 18-7-2005 04:21 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 18-7-2005 12:44 AM 发表
它的concept是要integrate一个函数f(x),范围在a到b (i.e. 0到1),就把 a ->b 的interval 分成 n 个区,使每个区的宽=(b-a)/n 。那么f(x)的积分也相等于把f(x)分为n个长方形的面积的和 。其和为 lim{ Sum f(x ...
这个方法叫做trapezium rule...
不能准确算出integration的值,但却是很好的estimation。
越小的"width"(也就是越多个trapeziums),就代表estimation更准确
我现在就在读这个concept |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-7-2005 05:08 PM
|
显示全部楼层
发表于 18-7-2005 05:08 PM
|
显示全部楼层
原帖由 無聊人 于 18-7-2005 04:21 PM 发表
这个方法叫做trapezium rule...
不能准确算出integration的值,但却是很好的estimation。
越小的"width"(也就是越多个trapeziums),就代表estimation更准确
我现在就在读这个concept
咦?Trapezium rule 不 是 另 一 个 吗? 不 管trapezium rules 也 好quadrature 也 好 , 这 方 法 把 " width" 分 成 无 限 多, 所 以 得 到 的 答 案 和integration 出 来 的 应 该 是 一 样 的。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-7-2005 09:57 PM
|
显示全部楼层
发表于 18-7-2005 09:57 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 18-7-2005 05:08 PM 发表
咦?Trapezium rule 不 是 另 一 个 吗? 不 管trapezium rules 也 好quadrature 也 好 , 这 方 法 把 " width" 分 成 无 限 多, 所 以 得 到 的 答 案 和integration 出 来 的 应 该 是 一 ...
我的問題再與第三各等於怎麼變成那個積分式.... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-7-2005 03:23 PM
|
显示全部楼层
发表于 19-7-2005 03:23 PM
|
显示全部楼层
原帖由 灰羊 于 18-7-2005 09:57 PM 发表
我的問題再與第三各等於怎麼變成那個積分式....

在多兄的题目里,1/n = h (比如a=0,b=1) , k/n = x_k 所以
f(x_k) = (1/1+x_k)^2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-7-2005 07:18 PM
|
显示全部楼层
发表于 21-7-2005 07:18 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-7-2005 04:57 PM
|
显示全部楼层
发表于 22-7-2005 04:57 PM
|
显示全部楼层
有點明白了
就是1/n是dx
1/n上面的1代表(1-0)... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-7-2005 06:12 PM
|
显示全部楼层
发表于 22-7-2005 06:12 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-7-2005 01:06 AM
|
显示全部楼层
发表于 23-7-2005 01:06 AM
|
显示全部楼层
看到一题不定积分,很不错哦!
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2005 12:37 AM
|
显示全部楼层
发表于 9-9-2005 12:37 AM
|
显示全部楼层
试试这题 :
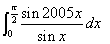
(pipi 提供) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-9-2005 05:35 PM
|
显示全部楼层
发表于 15-9-2005 05:35 PM
|
显示全部楼层
多谱勒的题目:

不知对吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-9-2005 10:10 PM
|
显示全部楼层
发表于 16-9-2005 10:10 PM
|
显示全部楼层
我有一题数学想请教各位。
Given that f(x)= (x+1)(x+2)...(x+10).
Find the coeffiecient of x^8 and x^9.
请问这题除了一个一个kembang出来之外,还有其它方法吗?? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-9-2005 11:28 PM
|
显示全部楼层
发表于 16-9-2005 11:28 PM
|
显示全部楼层
用违大定理(Vieta)可得x^9的系数为1+2+3+...+10=55
x^8的系数是 summation(ab)=1x2+1x3+1x4+..+2x3+2x4+...+9x10 ,暂时没想到较简单的机算方法...
*summation(ab)是所有ab的pattern的数的和 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-9-2005 05:42 PM
|
显示全部楼层
发表于 17-9-2005 05:42 PM
|
显示全部楼层
有了!,可以用
Sum(ab)=1\2 x{ (sum a)^2 - sum(a^2)}=1\2 x{55^2 - 385}
=1\2 x 2640 = 1320
*sum a=1+2+3+...+10=55
*sum a^2=1^2 + 2^2 + 3^2 + ...+ 10^2 = 385
所以coefficient of x^8 = 1320 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-9-2005 08:15 PM
|
显示全部楼层
发表于 18-9-2005 08:15 PM
|
显示全部楼层
多谱乐的题目另个解法
 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|