|
|

楼主 |
发表于 12-10-2004 12:20 PM
|
显示全部楼层
01/10/2004,星期五
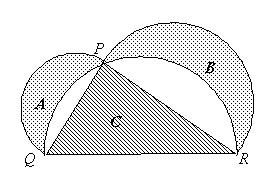
高中(B20) 如图,PQ,QR,RP 个别是个别圆的直径;而 A,B,C 则各为阴影部分的面积。
求证: A + B = C
 (已解) (已解)
(答案:--)
(解对者:fritlizt,eeCyang,sinchee,灰羊,38女)
解法(一)
QPR 是一个半圆。
所以角QPR = 90.
半圆PQ 的面积为 : pai * PQ^2 /8
半圆PR 的面积为 : pai * PR^2 /8
半圆RQ 的面积为 : pai * RQ^2 /8
有根据 phytagoras theorem, 半圆PQ 的面积 + 半圆PR 的面积 = 半圆RQ 的面积
再扣除白色的面积,
A+B = C
解法(二)
QPR 是一个半圆。
所以角QPR = 90.
半圆PQ 的面积为 : pai * (PQ/2)^2/2
半圆PR 的面积为 : pai * (PR/2)^2/2
半圆RQ 的面积为 : pai * (RQ/2)^2/2
结果得:[pai * (PQ/2)^2/2 + pai * (PR/2)^2/2 + pai * (RQ/2)^2/2]
-[pai * (PQ/2)^2/2 + pai * (PR/2)^2/2 + PQ*PR/2]
得 pai * (RQ/2)^2/2 -PQ*PR/2 这是白色的面积...
过后我才用左式证:
A+B= pai* (PQ/2)^2/2 + pai* (PR/2)^2/2 -[pai* (RQ/2)^2/2 -PQ*PR/2]
C= PQ*PR/2
那如果要令到A+B=C.. 那pai* (PQ/2)^2/2 + pai* (PR/2)^2/2= pai* (RQ/2)^2/2
这和phytagoras theorem很像...
解法(三)
設 PQ = a, PR = b, QR = c,
即 a,b,c 分別為三個半圓的直徑。
故 a^2 + b^2 = c^2
因為三個皆為半圓﹐即相似形。
而﹐ 相似形的面積比 = (邊比)^2
半圆 PQ 的面积 = (a^2/c^2) 半圆 QR 的面积
半圆 PR 的面积 = (b^2/c^2) 半圆 QR 的面积
因此﹐半圆 PQ 的面积 + 半圆 PR 的面积 = 半圆 QR 的面积
半圆 PQ 的面积 + 半圆 PR 的面积 - 空白部份 = 半圆 QR 的面积 - 空白部份
即 A + B = C。
解法(四)

[ Last edited by pipi on 12-10-2004 at 12:25 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:20 PM
|
显示全部楼层
02/10/2004,星期六
高中(B21) x 是任意实数,求证: cos(cos x) ≥ sin x 。 (已解)
(答案:--)
(解对者:sMIL3)
解法(一)
for cos(cosX):
when (cosX)=1(maximum),cos(cosX) is minimum
:.when X=0,cos(cosX) is minimum
:.cos(cos0)≦cos(cosX)≦1
:.cos1≦cos(cosX)≦1
如图:

解法(二)
若0≦x≦兀,則利用泰勒級數展開法
設cosx=t =>sinx= √(1-t^2),則原不等式變成cost≧√(1-t^2)
設cost的泰勒級數=f(t),√(1-t^2)的泰勒級數=g(t)
並令F(t)=f(t)-g(t)=>F’(t)=f’(t)-g’(t)
您將發現F’(t)≧0恆成立,此乃表示F(x)是遞增函數
∵-1≦t≦1,且F(-1)=0
∴cost≧√(1-t^2)
故cos(cosx)≧sinx
得證
解法(三)
用Maclaurin Series,
cos(t) = 1 - 1/2(cos t)^2 + 1/24 (cos t)^4 - ... for ∞<t<∞.
所以
cos(cosx)≥ 1 - 1/2(cos x)^2 (因为|cos x|≤1)
= 1/2 (2 - (cos x)^2)
= 1/2 (1 + (sin x)^2)
≧ sin x
[ Last edited by pipi on 12-10-2004 at 12:27 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:21 PM
|
显示全部楼层
07/10/2004,星期四
高中(B22)
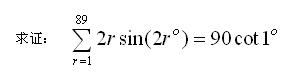 (已解) (已解)
(答案:--)
(解对者:sinchee)

[ Last edited by pipi on 12-10-2004 at 12:28 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:22 PM
|
显示全部楼层
08/10/2004,星期五
高中(B23) 有两堆棋子,数目相等.两人玩耍,每人可以在一堆里任意取几颗,但不能同时在两堆里取,规定取得最后一颗者胜。
求证后取者可以必胜。 (已解)
(答案:--)
(解对者:灰羊)
A先拿,無論A拿哪一堆的多少個,B在另一堆也拿相同數量(2堆數量相等)
持續下去,因為A先拿,所以A一定先拿完其中一堆,B勝
[ Last edited by pipi on 12-10-2004 at 12:28 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:22 PM
|
显示全部楼层
09/10/2004,星期六
高中(B24) 不许用计算机,试比较 e^π 与 π^e,哪个比较大? (已解)
(答案:e^π)
(解对者:sMIL3)
首先,证明 ln(x/lnX)≥1 for all x > 1:
y=ln(x/lnX) , x>1
dy/dx=(lnX-1)/(xlnX) , x>1
(e,1) is the minimum point lies on y
:.由此可知:
ln(π/lnπ)>1 (因为π>e)
lnπ-ln(lnπ)>1
lnπ>1+ln(lnπ)
lnπ>ln(elnπ)
π>elnπ
πlne>elnπ
ln(e^π)>ln(π^e)
:.e^π>π^e
[ Last edited by pipi on 12-10-2004 at 12:34 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-10-2004 10:24 AM
|
显示全部楼层
14/10/2004,星期四
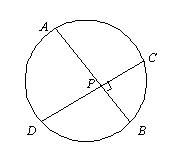
高中(B25) 如图,在圆 O 任意画二 互相垂直的(chord):AB 及 CD。
若 AB 与 CD 交点为 P 。
求证: AP^2 + PB^2 + CP^2 + PD^2 恒为某定值。
 (已解) (已解)
(答案:--)
(解对者:430201,灰羊)
解法(一)
设AP>PB,PD>PC,且圆O的半径为r
作OE⊥AB于E,OF⊥CD于F,又AB⊥CD,
则OE=PF,OF=PE,
且AE=BE,DF=CF
故AP^2 + PB^2 + CP^2 + PD^2
=(AE+EP)^2 + (BE-EP)^2 + (CF-PF)^2 + (DF+PF)^2
=AE^2 + EP^2 + BE^2 + EP^2 +CF^2 + PF^2 + DF^2 + PF^2
=2(AE^2+OE^2)+2(DF^2+OF^2)
=2OA^2+2OD^2=4r^2
解法(二)

[ Last edited by pipi on 19-10-2004 at 10:27 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-10-2004 10:24 AM
|
显示全部楼层
15/10/2004,星期五
高中(B26) 若 a^3 + b^3 = 2.
求证 a + b ≤ 2. (已解)
(答案:--)
(解对者:430201)
設a+b=k,其中k≠0(若k=0,則a^3 + b^3=0,與已知矛盾)
則a=k-b,代入a^3 + b^3 = 2.
化簡得3k(b^2)-3(k^2)b+(k^3-2)=0
∵k為實數
∴判別式=﹝-3(k^2)﹞^2-4×(b^2)×(k^3-2)≧0
化簡得k(k-2)(k^2+2k+4)≦0
∵k^2+2k+4=(k+1)^2+3>0
∴k(k-2) ≦0,又k≠0
則0<k≤ 2.
故本題得證
[ Last edited by pipi on 19-10-2004 at 10:28 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-10-2004 10:25 AM
|
显示全部楼层
16/10/2004,星期六
高中(B27) 已知 α 、β 为锐角,
且 3(sin α)^2 + 2(sin β)^2 = 1;
3(sin 2α) - 2(sin 2β) = 0,
求证: α + 2β = π/2 。 (已解)
(答案:)
(解对者:)

[ Last edited by pipi on 19-10-2004 at 10:28 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:55 PM
|
显示全部楼层
21/10/2004,星期四
高中(B28) 我们设
指令(1)为:由左到右,报数! 喊奇数的学生退出;喊偶数的学生保留,
指令(2)为:由右到左,报数! 喊奇数的学生退出;喊偶数的学生保留,
100 个学生排成一列。
指令(1)
指令(2)
指令(1)
指令(2)
...
如此指令重复,直到最后一个学生!
问:这最后一个学生第一次喊什么号码? (已解)
(答案:54)
(解对者:430201)
解法
第一次剩下2的倍數:2、4、6、8、…、100(50個)
第二次剩下型如2+4n的數:2、6、10、14、…、98(25個)
第三次剩下型如6+8n的數:6、14、22、30、…、94(12個)
第四次剩下型如6+16n的數:6、22、38、54、70、86(6個)
第五次剩下:22、54、86
第六次剩下:54
[ Last edited by pipi on 25-10-2004 at 04:05 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:55 PM
|
显示全部楼层
22/10/2004,星期五
高中(B29) 若 0< a,b < 1 ?
试求
√{a^2 + b^2} + √{(1-a)^2 + b^2} + √{(1-a)^2 + (1-b)^2} + √{a^2 + (1-b)^2}
的极小值。 (已解)
(答案:2√2)
(解对者:多普勒效应)
解法
利用构造法:
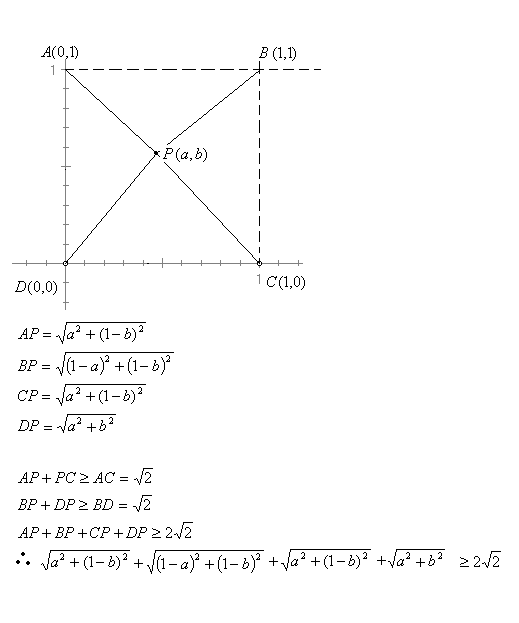
所以,极小值是 2√2
[ Last edited by pipi on 25-10-2004 at 04:07 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:56 PM
|
显示全部楼层
23/10/2004,星期六
高中(B30) 在三角形 ABC,角 C 为直角。
试求 (a+b)/c 的极大值及极小值。 (已解)
(答案:极大值=√2,没有 极小值...)
(解对者:多普勒效应)

没有极小值。
[ Last edited by pipi on 25-10-2004 at 04:19 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:37 PM
|
显示全部楼层
28/10/2004,星期四
高中(B31) 已知 a, b 为正整数,且 (a,b) 满足 10 < a^2 + b^2 < 28 。
问共有几组不同的 (a,b) ? (已解)
(答案:11)
(解对者:430201)
(1)若a=1
則9 < b^2 < 27
即3 < b < 6
∴b=4,5
(2)若a=2
則6 < b^2 < 24
即2 < b < 5
∴b=3,4
(3)若a=3
則1 < b^2 < 17
即1 < b < 5
∴b=2,3,4
(4)若a=4
則0 < b^2 < 12
即0 < b < 4
∴b=1,2,3
(5)若a=5
則0 < b^2 < 3
即0 < b < 2
∴b=1
故共有11組
[ Last edited by 多普勒效应 on 31-10-2004 at 09:34 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:37 PM
|
显示全部楼层
29/10/2004,星期五
高中(B32) (B32) 若 f(x) = (x-1)(x-2)(x-3)(x-4)…(x-10),
求 f '(10)。 (已解)
(答案:9!)
(解对者:ah_mok)
解法
设g(x) = (x-1)(x-2)(x-3)(x-4)…(x-9)
h(x) = (x-10)
f(x) = g(x)h(x)
f '(x) = g'(x)h(X)+g(x)h'(x)
= g'(x)(x-10) + g(x)(1)
f'(10) =g'(10)(10-10) + g(10)
= g(10)
=(10-1)(10-2)(10-3)(10-4)…(10-9)
=9(8)(7)(6)(5)(4)(3)(2)(1)
=9!
[ Last edited by pipi on 30-10-2004 at 07:58 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:38 PM
|
显示全部楼层
30/10/2004,星期六
高中(B33) 已知 x, y 为正整数,且 (x,y) 满足 1/x + 1/y = 1/30 。
求 y 的极大值。 (已解)
(答案:930)
(解对者:430201)
解法
∵1/x + 1/y = 1/30 。
去分母 30y+30x=xy
xy-30x-30y=0
x(y-30)-30(y-30)=900
(x-30)(y-30)=900
當x-30=1時,y-30有極大值900
故y的極大值為930
[ Last edited by pipi on 30-10-2004 at 07:59 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-11-2004 08:33 PM
|
显示全部楼层
发表于 5-11-2004 08:33 PM
|
显示全部楼层
04/11/2004,星期四
高中(B34)
证明 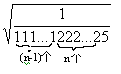
是有理数。 (已解)
(答案:--)
(解对者:萧晨 , 430201)
解法(一)
分母抽5--->2222...244444...45
(n-1个2,n-1个4,一个5)
再抽5--->444....4888...89
(n-1个4,n-2个8,一个9)
--->444...48888...8+1
(n-1个4,n-1个8)
在用数学归纳法证明这个式子是平方数
所以整个分母就是平方数
可以开更号然后倒数
解法(二)
設1111…1(共n-1個1)=A
則1111…1222…25
=A×10^(n+1)+2×A×10^2+25
=A×10^2×〔10^(n-1)+2〕+25
=A×10^2×(9A+3)+25
=9×A^2×10^2+A×10^2×3+25
=(3A×10)^2+2×(3A×10)×5+5^2
=(30A+5)^2
=(333…35)^2(共n-1個3)
故本題得証
[ Last edited by 多普勒效应 on 5-11-2004 at 08:36 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-11-2004 08:33 PM
|
显示全部楼层
发表于 5-11-2004 08:33 PM
|
显示全部楼层
05/11/2004,星期五
高中(B35)
解方程
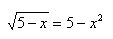
(已解)
(答案:1/2 (– 1 + √21) 或 1/2 (1 - √17))
(解对者:萧晨,sinchee)
解法(一)
用 linear interpolation
Answer=1.791284544 , -1.561548897
解法(二)
两边平方,得:
x^4 – 10x^2 + x + 20 = 0
(x^2 + x – 5)(x^2 – x – 4) = 0
x = 1/2 (– 1 ± √21) or 1/2 (1 ± √17)
经检验,
x = 1/2 (– 1 + √21) or 1/2 (1 - √17)
解法(三)
设 a=5,两边平方得 x^4 - 2ax^2 + x + a^2 - a = 0
a^2 - (2x^2 +1)a + x^4 + x = 0
判别式 = (2x-1)^2
用公式法得 a1 = x^2 + x , a2 = x^2 - x +1
接下来的就和解法(二)一样。
[ Last edited by 多普勒效应 on 5-11-2004 at 08:43 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-11-2004 08:34 PM
|
显示全部楼层
发表于 5-11-2004 08:34 PM
|
显示全部楼层
06/11/2004,星期六
高中(B36)
x,y,z 都是正整数,且
x + [y] + {z} = 13.2
[x]+{y}+ z = 14.3
{x}+y+[z] = 15.1
求 x,y,z 之值。
(已解)
(答案:)
(解对者:430201)
解法(一)
∵x + [y] + {z} = 13.2
[x]+{y}+ z = 14.3
{x}+y+[z] = 15.1
∴(一)[x]+{x}+[y]+{z}=13.2
則[x]+[y]=13,{x}+{z}=0.2
或[x]+[y]=12,{x}+{z}=1.2
(二)[x]+{y}+[z]+{z}=14.3
則[x]+[z]=14,{y}+{z}=0.3
或[x]+[z]=13,{y}+{z}=1.3
(三){x}+[y]+{y}+[z]=15.1
則[y]+[z]=15,{x}+{y}=0.1
或[y]+[z]=14,{x}+{y}=1.1
可能有8組解
(1)[x]+[y]=13,[x]+[z]=14,[y]+[z]=15
且{x}+{z}=0.2,{y}+{z}=0.3,{x}+{y}=0.1
解之得,x=6、y=7.1、z=8.2
(2)[x]+[y]=13,[x]+[z]=14,[y]+[z]=14
且{x}+{z}=0.2,{y}+{z}=0.3,{x}+{y}=1.1
得,[x]+[y]+[z]=20.5(不合)
(3)[x]+[y]=13,[x]+[z]=13,[y]+[z]=15
且{x}+{z}=0.2,{y}+{z}=1.3,{x}+{y}=0.1
得,[x]+[y]+[z]=20.5(不合)
(4)[x]+[y]=13,[x]+[z]=13,[y]+[z]=14
且{x}+{z}=0.2,{y}+{z}=1.3,{x}+{y}=1.1
解之得,{y}=1.1(不合)
(5)[x]+[y]=12,[x]+[z]=14,[y]+[z]=15
且{x}+{z}=1.2,{y}+{z}=0.3,{x}+{y}=0.1
得,[x]+[y]+[z]=20.5(不合)
(6)[x]+[y]=12,[x]+[z]=14,[y]+[z]=14
且{x}+{z}=1.2,{y}+{z}=0.3,{x}+{y}=1.1
解之得,{x}=1(不合)
(7)[x]+[y]=12,[x]+[z]=13,[y]+[z]=15
且{x}+{z}=1.2,{y}+{z}=1.3,{x}+{y}=0.1
解之得,{z}=1.2(不合)
(8)[x]+[y]=12,[x]+[z]=13,[y]+[z]=14
且{x}+{z}=1.2,{y}+{z}=1.3,{x}+{y}=1.1
得,[x]+[y]+[z]=19.5(不合)
解法(二)
把三个等式相加 :
2(x+y+z)=42.6 => x+y+z = 21.3 ----(4)
(4) - (1) => y-[y]+z-{z}= [z] + {y} = 8.1 => [z]=8 , {y}=0.1
同理 ,(4) - (2) => [y]+{x} = 7 => [y]=7 ,{x}=0
(4) - (3) => [x] + {z} =6.2 => [x]=6 . {z}=0.2
[ Last edited by 多普勒效应 on 19-11-2004 at 12:26 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:18 AM
|
显示全部楼层
发表于 19-11-2004 12:18 AM
|
显示全部楼层
11/11/2004,星期四
高中 (B37)
f 和 g 是两个多项式(polynomial),且
f(x + g(y))=3x + y + 4
给所有实数x,y
求 g( 8 + f (3)) 之值。
(待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:20 AM
|
显示全部楼层
发表于 19-11-2004 12:20 AM
|
显示全部楼层
12/11/2004,星期五
高中 (B38)
a,b 是 x^2 - (k-1)x + (k^2 + 3k +4)=0
的两根,k 是某些实数。
求 a^2 + b^2 的最大值。
(已解)
(答案:8)
(解对者:灰羊,430201)
解法(一)
(1)若兩根a、b為任意數
a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9 ≦9
故 a^2 + b^2 的最大值是9
(2)若兩根a、b為任意實數
∵兩根a、b為任意實數
∴判別式=(k - 1)^2 - 4(k^2 + 3k + 4)≧0
解得 -3≦k≦-5/3
又a^2 + b^2 =(a+b)^2 - 2ab
=(k-1)^2 - 2(k^2 + 3k +4)
=-(k+4)^2 + 9
則81/9≦(a^2 + b^2)≦8
故 a^2 + b^2 的最大值是8
[ Last edited by 多普勒效应 on 19-11-2004 at 12:29 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:22 AM
|
显示全部楼层
发表于 19-11-2004 12:22 AM
|
显示全部楼层
13/11/2004,星期六
高中 (B39)
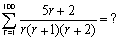
(已解)
(答案:15200/5151)
(解对者:灰羊)
解法(一)

解法(二)
simplified (5r+2)/r(r+1)(r+2)
===>5r/r(r+1)(r+2) + 2/r(r+1)(r+2)
= 5/(r+1)(r+2) + 2/r(r+1)(r+2)----〉做法在下面
= 5[1/(r+1) - 1/(r+2)] + 2[1/r - 1/(r+1)] - [1/r - 1/(r+2)]
然后summation
=5{1/2-1/102} + 2{1/1-1/101} - {1/1+1/2-1/101-1/102}
=125/51 + 200/101 - 7625/5151
=15200/5151
另外simplify 1/r(r+1)(r+2)
===>[1/r] [1/(r+1)(r+2)]
===>[1/r] [1/(r+1) - 1/(r+2)]
===>[1/r(r+1)] - [1/r(r+2)]
===>[1/r - 1/(r+1)] - [1/r - 1/(r+2)]/2
[ Last edited by 多普勒效应 on 19-11-2004 at 12:32 AM ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|